| Art | Wann | Wo | Beginn | LP | Dozent |
|---|---|---|---|---|---|
| V4 | Dienstag 12:30 -14:00 Donnerstag 12:30 - 14:00 | AVZ III / HS 1 AVZ III / HS 1 | 15. Oktober 2013 | 5,5 | Röglin |
| Ü2 | Termine | 21. Oktober 2013 | 3,5 | Bruckschen, Brunsch, Loka, Omlor, Rösner, Schäfer, Seume | |
Die Ergebnisse der Nachklausur können nun in Basis eingesehen werden. Die Einsicht findet am 7. April zwischen 13:00 und 13:45 Uhr in Raum E.08 im LBH statt.
In dieser Vorlesung werden wir uns mit dem Entwurf und der Analyse von Algorithmen beschäftigen. Ein Algorithmus ist eine Handlungsvorschrift zur Lösung eines Problems, die so präzise formuliert ist, dass sie von einem Computer ausgeführt werden kann. Algorithmen sind heute so allgegenwärtig, dass sie kaum wahrgenommen oder gewürdigt werden. Wie selbstverständlich nutzen wir Navigationsgeräte, um den besten Weg vom Start zum Ziel zu bestimmen, oder Suchmaschinen, um innerhalb kürzester Zeit riesengroße Datenmengen zu durchsuchen. Dass dies überhaupt möglich ist, liegt zum Teil an der immer besseren Hardware, zu einem viel größeren Teil liegt es aber an den cleveren Algorithmen, die für diese Anwendungen entwickelt wurden. In dieser Vorlesung werden wir Techniken zum Entwurf und zur Analyse von Algorithmen kennenlernen und diese nutzen, um effiziente Algorithmen für zahlreiche grundlegende Probleme zu entwerfen.
| Datum | Inhalt | Literatur |
|---|---|---|
| 15. Oktober | 1 Einleitung 1.1 Grundbegriffe 1.2 Ein erstes Beispiel: Insertionsort | Folien Skript |
| 17. Oktober | 1.2 Ein erstes Beispiel: Insertionsort (Fortsetzung) 1.3 Registermaschinen 1.4 Größenordnungen | Skript |
| 22. Oktober | 2 Methoden zum Entwurf von Algorithmen 2.1 Divide-and-Conquer 2.1.1 Mergesort | Skript |
| 24. Oktober | 2.1.2 Strassen-Algorithmus 2.1.3 Lösen von Rekursionsgleichungen | Skript |
| 29. Oktober | 2.2 Greedy-Algorithmen 2.2.1 Optimale Auswahl von Aufgaben | Skript |
| 31. Oktober | 2.2.2 Rucksackproblem mit teilbaren Objekten | Skript |
| 5. November | 2.2.2 Rucksackproblem mit teilbaren Objekten (Fortsetzung) 2.3 Dynamische Programmierung 2.3.1 Berechnung optimaler Zuschnitte | Skript |
| 7. November | 2.3.1 Berechnung optimaler Zuschnitte (Fortsetzung) 2.3.2 Rucksackproblem | Skript |
| 12. November | 3 Sortieren 3.1 Quicksort 3.2 Eigenschaften von Sortieralgorithmen | Skript |
| 14. November | 3.3 Untere Schranke für die Laufzeit vergleichsbasierter Sortieralgorithmen 3.4 Sortieren in Linearzeit | Skript |
| 19. November | 4 Dynamische Mengen 4.1 Felder und Listen 4.2 Suchbäume | Skript |
| 21. November | 4.2.1 AVL-Bäume | Skript |
| 26. November | 4.2.1 AVL-Bäume (Fortsetzung) 4.2.2 B-Bäume | Skript |
| 28. November | 4.2.2 B-Bäume (Fortsetzung) 4.3 Hashing | Skript |
| 3. Dezember | 4.3.1 Hashfunktionen 4.3.2 Hashing mit verketteten Listen | Skript |
| 5. Dezember | 4.3.3 Geschlossenes Hashing | Skript |
| 10. Dezember | 4.3.3 Geschlossenes Hashing (Fortsetzung) 5 Graphenalgorithmen 5.1 Tiefen- und Breitensuche 5.1.1 Tiefensuche | Skript |
| 12. Dezember | 5.1.1 Tiefensuche (Fortsetzung) 5.1.2 Breitensuche | Skript |
| 17. Dezember | 5.1.2 Breitensuche (Fortsetzung) 5.2 Minimale Spannbäume 5.2.1 Union-Find-Datenstrukturen | Skript |
| 19. Dezember | 5.2.1 Union-Find-Datenstrukturen (Fortsetzung) 5.2.2 Algorithmus von Kruskal | Skript |
| 7. Januar | 5.3 Kürzeste Wege 5.3.1 Grundlegende Eigenschaften von kürzesten Wegen 5.3.2 Single-Source Shortest Path Problem | Skript |
| 9. Januar | 5.3.2 Single-Source Shortest Path Problem (Fortsetzung) 5.3.3 All-Pairs Shortest Path Problem | Skript |
| 14. Januar | 5.4 Flussprobleme 5.4.1 Anwendungsbeispiele 5.4.2 Algorithmus von Ford und Fulkerson | Skript |
| 16. Januar | 5.4.2 Algorithmus von Ford und Fulkerson (Fortsetzung) 5.4.3 Algorithmus von Edmonds und Karp | Skript |
| 21. Januar | 5.4.3 Algorithmus von Edmonds und Karp (Fortsetzung) 6 Lineare Programmierung | Skript |
| 23. Januar | 6.1 Grundlagen 6.1.1 Kanonische Form und Gleichungsform 6.1.2 Geometrische Interpretation | Skript |
| 28. Januar | 6.1.2 Geometrische Interpretation (Fortsetzung) 6.1.3 Algebraische Interpretation | Skript |
| 30. Januar | 6.2 Simplex-Algorithmus 6.2.1 Formale Beschreibung 6.2.2 Berechnung der initialen Basislösung 6.2.3 Laufzeit 6.3 Komplexität von linearer Programmierung | Skript |
| 4. Februar | 7 Kontextfreie Sprachen 7.1 Sprachen und Grammatiken 7.2 Chomsky-Normalform und der Cocke-Younger-Kasami-Algorithmus | Skript |
| 6. Februar | 7.2 Chomsky-Normalform und der Cocke-Younger-Kasami-Algorithmus (Fortsetzung) 7.3 Pumping-Lemma für kontextfreie Sprachen | Skript |
Für den Erhalt des Übungsscheins müssen insgesamt mindestens 50% der zu erreichenden Punkte bei den Übungsaufgaben erreicht werden und Lösungen von drei Aufgaben müssen im Laufe des Semesters erfolgreich in den Tutorien präsentiert werden. Eine Abgabe der Übungsaufgaben in Gruppen bis zu drei Studierenden ist möglich.
| Wann | Wo | Tutor | |
|---|---|---|---|
| 1 | Montag 8:15 - 9:45 | AVZ III / A301 | Yvonne Omlor |
| 2 | Montag 12:15 - 13:45 | AVZ III / A6c | Patrick Loka |
| 3 | Montag 12:15 - 13:45 | AVZ III / A7a | Patrick Seume |
| 4 | Montag 12:15 - 13:45 | AVZ III / A7b | Tobias Brunsch |
| 5 | Montag 14:15 - 15:45 | AVZ III / A7a | Patrick Seume |
| 6 | Dienstag 8:15 - 9:45 | AVZ III / A301 | Yvonne Omlor |
| 7 | Mittwoch 12:15 - 13:45 | AVZ III / A301 | Patrick Loka |
| 8 | Mittwoch 12:15 - 13:45 | AVZ III / A7a | Clemens Rösner |
| 9 | Donnerstag 8:15 - 9:45 | AVZ III / A7a | Philipp Bruckschen |
| 10 | Donnerstag 10:15 - 11:45 | AVZ III / A301 | Philipp Bruckschen |
| 11 | Freitag 10:15 - 11:45 | AVZ III / A7a | Sonja Schäfer |
| 12 | Freitag 12:15 - 13:45 | AVZ III / A301 | Sonja Schäfer |
Die Anmeldung zu den Übungsgruppen erfolgt über das Tutorienvergabesystem (TVS). Eine einmalige Registrierung ist vom Netz der Universität Bonn aus erforderlich. Anschließend können Sie von überall auf das TVS zugreifen und bis einschließlich Freitag, den 18. Oktober, Ihre Wunschtermine angeben.
Die Klausur findet am 18.2.2014 um 9 Uhr im Hörsaal X im Uni-Hauptgebäude statt. Die Nachklausur findet am 20.3.2014 um 9 Uhr im Hörsaal X im Uni-Hauptgebäude statt. Zur Vorbereitung auf die Klausur haben wir eine Probeklausur online gestellt.
Nachfolgend finden Sie den Notenspiegel der Klausur.
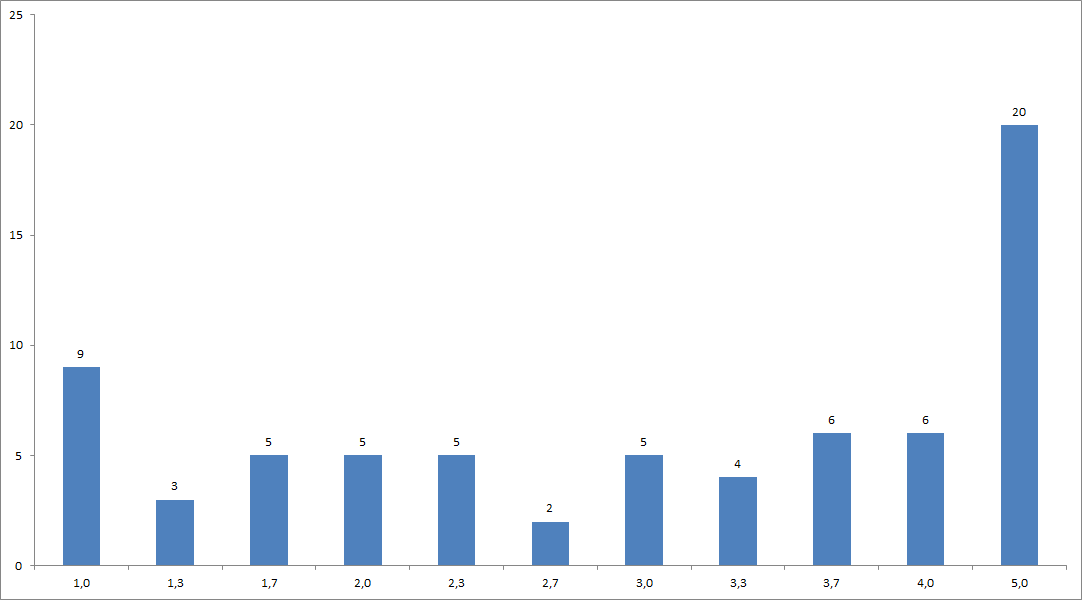
Die Inhalte der Vorlesung finden sich in diesem Skript, das während des Semesters kontinuierlich erweitert wird.
Die Vorlesung basiert in wesentlichen Teilen auf der folgenden Literatur:
Weiterführende Literatur: